Modul manajemen matematika ekonomi

Hello friends Tensei Shitara Slime Datta Ken, on this occasion the admin wants to share an article entitled Modul manajemen matematika ekonomi - Fungsi, we have made good, quality and useful articles for you to read and take information in. hopefully the post content is about materi, modul-mme, which we write you can understand. Alright, happy reading.

PERTEMUAN KE- 9 POKOK BAHASAN FUNGSI

A. TUJUAN PEMBELAJARAN :

Adapun tujuan pembelajaran yang akan dicapai setelah Anda mempelajari modul ini, secara khusus Anda diharapkan dapat:

1.1. Mendiskripsikan dan mengidentifikasikan konstan, dan variabel.

1.2. Menggambar grafik suatu fungsi.

B. URAIAN MATERI

FUNGSI

PENGERTIAN DAN UNSUR-UNSUR FUNGSI

Fungsi ialah suatubentuk hubungan matematisyang menyatakan hubungan ketergantungan (hubungan fungsional) antara satu variabel dengan variabel lain.sebuah fungsi dibentuk oleh beberapa unsur. Unsur-unsur pembentuk fungsi adalah variabel, koefisien dan konstanta. Variabel dan koefisien senantiasa terdapat dalam setiap bentuk fungsi.Akan tetapi tidak demikiannya dengan konstanta. Sebuah fungsi yang secara kongket dinyatakan dalam bentuk persamaan dan pertidaksamaan, mungkin sekali mengandung sebuah konstanta dan mungkin juga tidak mengandung konstanta. Walaupun sebuah persamaan atau pertidaksamaan tidak mengandung konstanta, tidaklah mengurangi artinya sebuah fungsi.

Variabel ialah unsur pembentuk fungsiyang mencerminkan atau mewakili faktor tertentu, dilambangkan (berdasarkan kesepakatan umum) dengan huruf huruf latin. Dalam matematika, variabel-variabel dalam sebuah persamaan lazimnya ditulis dalam huruf-huruf kecil, melambangkan sumbu-sumbu dalam sistem koordinat (absis dan ordinat). Dalam ekonomi tidak terdapat ketentuan bahwa variabel dalam suatu persamaan harus dituliskan dengan huruf kecil. Berdasarkan kedudukan atau sifatnya, didalam setiap fungsi terdapat dua macam variabel yaitu variabel bebas dan variabel terikat. Variabel bebas (independent variable) ialahvariabel yang nilainyatidak tergantung pada variabel lain,

Fungsi polinm ialah fungsi yang mengandung banyak suku (polinom) dalam variabel bebasnya. Pangkat tertinggi pada variabel suatu fungsi polinom mencerminkan derajat polinornnya, sekaligus juga mencerminkan derajat persamaan atau fungsi tersebut.
Bentuk umum fungsinya:

Fungsi linear ialah fungsi polinom khusus yang pangkat tertinggi dari variabelnya adalah pangkat satu, sehingga sering juga disebut fungsi berderajat satu.
Bentuk umum fungsinya: Dimana: ao adalah konstanta dan nilai

Fungsi non-linier (fungsi kuadrat, fungsi kubik, fungsi bikuadrat, dan sebagainya) yaitu fungsi-fungsi yang pangkat tertinggi lebih dari satu.

Fungsi kuadrat ialah fungsi polinom yang pangkat tertinggi dari variabelnya
adalah pangkat dua dan sering juga disebut fungsi berderajat dua. Bentuk umum fungsinya:
Dimana: ao adalah konstanta
a1 dan a2 adalah koefisien dan nilai

Fungsi berderajat n ialah fungsi yang pangkat tertinggi dari variabelnya adalah pangkat n (dimana n merupakan bilangan nyata)
Bentuk umum fungsinya: Dimana:
ao adalah konstanta
a1 dan an adalah koefisien dan nilai

Fungsi pangkat ialah fungsi yang variabel bebasnya berpangkat bilangan nyata yang bukan nol.
Bentuk umum fungsinya: Y = Xⁿ
Dimana : n = bilangan nyata dan .

Fungsi eksponensial ialah fungsi yang variabel bebasnya merupakan pangkat dari suatu konstanta bukan nol.
Bentuk umum fungsinya: Y = xn
Dimana : n = bilangan nyata dan n > 0.

Fungsi logaritmik ialah fungsi balik (inserve) dari fungsi eksponensial variabel bebasnya merupakan bilangan logaritmik.
Bentuk urnurn fungsinya: Y = nLog X

Fungsi trigonometrik dan fungsi hiperbolik ialah fungsi yang variabel bebasnya rnerupakan bilangan-bilangan goneornetrik.
Bentuk urnurn fungsi trigonometric: Y = Sin 5X Bentuk urnurn fungsi hiperbolik: Y = arc Cos 2X

Berdasarkan letak ruas variabel-variabelnya (x dan y), fungsi dibedakan rnenjadi dua jenis, yaitu:

1. Fungsi eksplisit yaitu fungsi yang variabel bebas (x) dan variabel terikatnya (y) terletak pada ruas yang berlainan.

2. Fungsi irnplisit yaitu fungsi yang variabel bebas (x) dan variabel terikatnya (y) terletak pada ruas yang sarna, baik sebelah kiri rnaupun sebelah kanan. Berikut ini bentuk operasional dari kedua fungsi di atas:

MENGGAMBARKAN GRAFIK FUNGSI LINIER

Setiap fungsi dapat disajikan secara grafik pada bidang sepasang surnbu silang (sistern koordinat). Garnbar dari sebuahfungsi dapat dihasilkan dengan cara rnenghitung koordinat titik-titik yang rnernenuhi persarnaannya, dan kernudian rnernindahkan pasangan-pasangan titik tersebut ke sistern surnbu silang. Dalarn rnenggarnbarkan suatu fungsi rneletakkan variabel bebas pada surnbu horizontal (absis) dan variabel terikat pada sumbu vertikal (ordinat).

Bentuk Urnurn Fungsi Linier:

y = a + bx atau y = rnx + c

Dirnana:

aatau c adalah konstanta atau potongan (intercept) garispada surnbu vertikaly.

b atau m merupakan koefisien arah/lereng (slap e)/kemiringan/gradien garisnya. Koefisien nilai b atau m mencerminkan:

■ Besar tambahan nilai y untuk setiap tambahan satu unit x,

■ Tangen dari sudut yang dibentuk oleh garis y dan sumbu x.

(Catatan: koefisien arah dari sutu fungsi kinier selalu konstan, untuk setiap x)

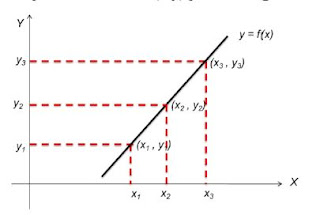
Gambar dari sebuah fungsi dapat dihasilkan dengan cara menghitung koordinat titik-titik yang memenuhi persamaannya dan kemudian memindahkan pasangan pasangan titik tersebut ke dalam sistem koordinat kartesius, dimana sumbu horizontal (absis) merupakan letak dari nilai variabel bebasnya (x) dan sumbu vertical (ordinat) merupakan letak dari nilai variabel terikatnya (y).

Untuk menggambarkan grafik sebuah fungsi y = f(x), maka grafiknya adalah himpunan semua titik (x,y) pada bidang.

Contoh:

Gambarkanlah grafik dari fungsi linier berikut ini:

a. y= 3 + 2x

b. y= 8 - 2x Penyelesaian:

a. Untuk fungsi linier y = 3 + 2x , nilai konstanta a = 3 dan koefisien arah (b)

= 2. Perlu diperhatikan apabila koefisien arah b bemilai positif (b>0), maka grafik garisnya kan bergerak dari kiri bawah ke kanan atas.

Pasangan berurutan fungsi y = 3 + 2x

Jika Nilai x	Nilai y = 3 + 2x	Pasangan bilangan (x,y)
x=0	y = 3 + 2 (0) = 3	( 0, 3)

Jika Nilai x	Nilai y = 3 + 2x	Pasangan bilangan (x,y)
x=l	y = 3 + 2 (1) = 5	( 1, 5)
x=2	y = 3 + 2 (2) = 7	( 2, 7)
x=3	y = 3 + 2 (3) = 9	( 3, 9)
x=4	y = 3 + 2 (4) = 11	( 4, 11 )

Grafik fungsinya

b. Untuk fungsi linier y = 8 - 2x , nilai konstanta a= 8 dan koefisien arah (b)

= -2. Karena koefisien arah b bemilai negatif (b < 0), rnaka grafik garisnya kan bergerak dari kiri atas ke kanan bawah.

Pasangan berurutan fungsi y = 3 + 2x

Jika Nilai x	Nilai y = 8 - 2x	Pasangan bilangan (x,y)
x=0	y = 8 - 2 (0) = 8	( 0, 8)
x=l	y=8 - 2(1)=6	( 1, 6)
x=2	y = 8 - 2 (2) = 4	( 2, 4)
x=3	y = 8 - 2 (3) = 2	( 3, 2)
x=4	y=8 - 2(4)=0	( 4, 0)

Grafik fungsi -> y = 8 - 2x

MENGGAMBARKAN GRAFIK FUNGSI NON-LINIER

Untuk menggambarkan grafikfungsi non liniertidaklah semudah menggambarkan grafik fungsi linier, hal ini dikarenakan masing-masing fungsi non linier memiliki bentuk khas tertentu mengenai kurvanya, sehingga diperlukan ketelitian dalam pembuatan grafiknya.

Berikut ini disajikan beberapa bentuk gambar dari beberapa fungsi non-linier:

1. Menggambar Funsi Kuadrat

Bentuk Umum fungsi kuadrat:

Contoh:
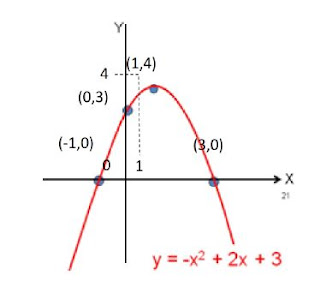
Gambarkan grafik fungsi dari y = -x² + 2x + 3

Jawab:

Jika Nilai x	Nilai y = -x² + 2x + 3	Pasangan bilangan (x,y)
X = -1	y = -(-1)² + 2(-1) + 3 = 0	( -1, 0)
x=0	y = -(0)² + 2(0) + 3 = 3	( 0, 3)
x=l	y=-(1)² +2(1)+3=4	( 1, 4)

Jika Nilai x	Nilai y = -x² + 2x + 3	Pasangan bilangan (x,y)
x=2	y = -(2)² + 2(2) + 3 = 3	( 2, 3)
x=3	y = -(3)² + 2(3) + 3 = 0	( 3, 0)

Grafik fungsi kuadrat dari y = -x²+ 2x + 3

2. Menggambar Grafik Fungsi Kubik

Contoh:

Gambarkan grafik fungsi dari y = -2 + 4x² _- x³ Jawab:

Grafik dari fungsi y = -2 + 4x2 - x3

3. Menggambar Grafik FungsiEksponensial

Gambarkan grafik fungsi dari y = (1/2)x

Grafik fungsi eksponen:

C. LATIHAN SOAL/TUGAS

Gambarkan grafik fungsi linear dan fungsi kuadrat berikut berikut :

1. y = 8 + 3x

2. y=2x+ 10

3. y= 10-4x

4. y = 5x-10

5. y = 6 - 2x + x2

6. Gambarkan grafik berikut ini dengan menggunakan tabel:

a. f(x) = 2/x ;jika 1 :S x :S 4

b. f(x) = 2x - 1 , jika 2 :S x :S 4

c. y = x² + 4x - 3 ; jika -2 :S x :S 1

7. Gambarkan grafik dari fungsi eksponen y = 2x.

*****

Download Modul .pdf

D. DAFTARPUSTAKA

Badrudin, R. & Algifari. 2003. Matematika Bisnis. Yogyakarta: BPFE

y ogyakarta.

Dumairy, 2010. Matematika Terapan untuk Bisnis dan Ekonomi, BPFE, Yogyakarta.

Danang Sunyoto, Matematika Ekonomi, Ardana, Yogyakarta, 2007.

Kalangi, JB. 2005, Matematika Ekonomi dan Bisnis, Jilid 1. Cetakan kelima.

Jakarta: Salemba Empat.

Silaen, S.. 2011, Matematika untuk Bisnis dan Ekonomi, Jakarta: Mitra Wacana Media.

Supranto. J, Matematika untuk Bisnis dan Ekonomi, Universitas Indonesia, Jakarta, 2002.

That's the article: Modul manajemen matematika ekonomi - Fungsi

Thank you for visiting my blog, hopefully it can be useful for all of you. Don't forget to share this article with your friends so they also know the interesting info, see you in other article posts.

You are now reading the article Modul manajemen matematika ekonomi - Fungsi with link address https://tenseishitaraslimedattakennews.blogspot.com/2020/05/modul-manajemen-matematika-ekonomi_36.html

Modul manajemen matematika ekonomi - Fungsi